オントラックの財務モデリング担当 北川です。
今日は「元金均等返済と元利均等返済のモデル化」について、ご紹介します。
一般的に借入金の返済方法には、二つの方法があります。
一つが元金の返済を同じ金額ずつしていく「元金均等返済」で、もう一つが元金返済と支払利息の合計が同じ金額となるように返済していく「元利均等返済」です。
財務モデルを作成したことがなくても、住宅ローンを借りたことがある人は聞いたことがあるかもしれません。
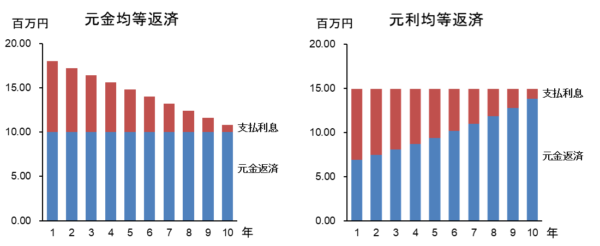
「元金均等返済」は、元金の返済がずっと同じ金額であり、借入残高の多い返済開始時には金利の支払が多くなるため元利支払額が最も多くなり、年々元利支払額が減っていく返済方法です。
一方、「元利均等返済」は、元利支払の額は一定ですので、返済開始時の支払額のうち大半が金利支払にあてられるため、借入金残高の減り方が遅い返済方法です。
今、100百万円(1億円)の借入をしたとして、利率は8%で固定、今後10年間で返済するとします。
この時、今後10年間の借入金残高の推移を見るために、どのようにしてモデルを作成するか、ご紹介します。
まずは、元金均等返済の場合を見てみましょう。
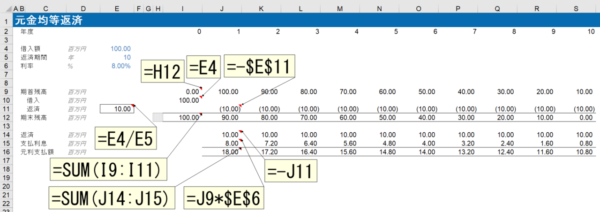
期首残高は前年の期末残高をリンクします。
借入は、最初の年(0年度)に借入額をリンクします。
元金均等返済の場合は、元金の返済額が一定ですので、毎年の返済額は100百万円/10年で10百万円となります。
期首残高に借入、返済を加味すると、期末残高が求まります。
ここでは、支払利息は期首残高に金利をかけて求めています。
次に、元利均等返済の場合を見てみましょう。
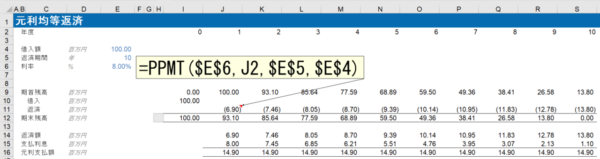
元利均等返済の場合の返済額の算出にはPPMT関数を用います。
PPMT関数の書式は、PPMT(利率、期、期間、現在価値、[将来価値]、[支払期日])
利率は、投資期間を通じて一定の利率(金利)を指定します。
期は、元金支払額を求める期を指定します。つまり、返済開始から何期目にあたるかを指定します。
期間は、投資期間全体での支払回数の合計(返済期間)を指定します。
現在価値は、将来行われる一連の支払を現時点で一括払いした場合の合計金額を言います。これは、返済開始時における借入残高にあたります。
将来価値は省略可能です。最後の支払を行った後に残る現金の収支を指定します。省略した場合は、ゼロとみなされます。
支払期日も省略可能です。いつ支払いが行われるかを、数値の0または1で指定します。0または省略した場合は各期の期末、1を指定した場合は各期の期首に支払いを行うこととなります。
元金均等返済のモデルから、返済の部分だけPPMT関数を使って修正すると、元利均等返済のモデルが完成です。
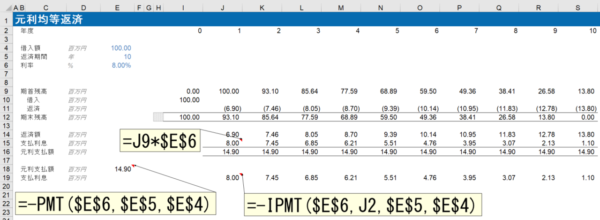
支払利息と返済額を足した元利支払額を見てみると、元利支払額がどの年も同じ金額になっていることがわかると思います。
PPMT関数に似た関数として、PMT関数、IPMT関数があります。
PMT関数では元利均等返済の支払利息+元金返済額である元利支払額、IPMT関数では同じく元利均等返済の支払利息額が算出されます。
元利均等返済の場合の元利支払額は期に関わらず一定ですので、PMT関数の書式は、PPMT関数の引数から「期」だけなくなり、PMT(利率、期間、現在価値、[将来価値]、[支払期日])となり、IPMT関数の書式は、PPMT関数と同じで、IPMT(利率、期、期間、現在価値、[将来価値]、[支払期日])となります。
PPMT関数も含め、求められる数字の符号がマイナスになる点には注意してください。
IPMT関数については、支払期日の指定に合わせて期首または期末の借入残高に利率を掛けても結果は同じですので、関数を使う必要はあまりないかもしれません。
ちなみに、ここでは年次のモデルを作成しましたが、月次のモデルを作成する場合は、利率は年利を12で割ったものを指定し、期や期間は月単位で指定します。
エクセルのスキルアップで働き方改革を!
次回の財務モデリング基礎講座は9月15日(日)です。お申し込みはこちらからどうぞ。